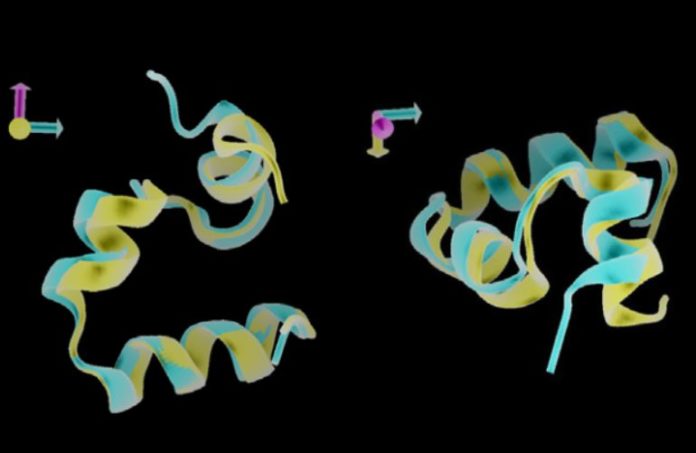Scientists from the University of Tel Aviv have developed a method with which you can quickly and accurately estimate the entropy of the system without resorting to additional considerations. To do this, the researchers displayed the system in a one-dimensional line, calculated the degree to which it can be compressed without loss, and displayed the resulting value in entropy. On five model examples in which the entropy can be calculated accurately, the error of the algorithm did not exceed several per cent. In addition, scientists have shown that using the proposed algorithm it is possible to solve the problem of protein folding.
To grasp the basic thermodynamic properties of the system, it is enough to know two functions – the entropy and enthalpy of the system. Roughly speaking, entropy measures the ordering of system elements, and enthalpy measures the energy that is needed to maintain its structure. To estimate the enthalpy, it is enough to know the strength of the interaction between the components of the system, therefore, usually, there are no problems with calculating this function. At the same time, to calculate the entropy, it is necessary to find the probabilities with which all possible microstates of the system are realized (for example, various methods of protein folding). As the size of the system increases, the complexity of this task grows rapidly, and even large supercomputers cannot solve it for large systems. To evaluate the properties of such systems, scientists have to go-to tricks.
In particular, one way to estimate the entropy of a complex system is based on the use of some a priori knowledge and assumptions – for example, empirical data accumulated in experiments with similar systems. This allows you to “trim” the space that you need to simulate a computer. Unfortunately, for each task the method of “cutting” is different. Other algorithms rely on methods that evaluate the distribution of work during the calculation or consider relationships between different areas of the phase space. However, in these methods, it is also impossible to distinguish a clear leader, and in many cases, the effectiveness of their work also greatly depends on the task.
A group of researchers led by Roy Beck has developed an algorithm that fairly accurately estimates the asymptotic entropy of an arbitrary system but requires relatively little computation. For this, the scientists noticed that the entropy of the system is proportional to the extent to which it is possible to compress a string of characters without loss, fully describing a given configuration. Roughly speaking, the greater the entropy of the system, the more difficult it is to single out any regularities in it; if there are no such patterns, it is impossible to “squeeze” information about the system without loss. It remains to figure out how to correctly map a system to a string, which in the general case is described by a large number of continuous degrees of freedom.
To build such a mapping, scientists followed the following sequence of actions. Researchers first identified relevant degrees of freedom of the system. For example, when calculating configurational entropy, scientists did not take into account the rotation and translation of the system. To simplify the calculations, each continuous coordinate (for example, an angle) was replaced by scientists with an approximate, discrete-changing coordinate (the so-called coarse–grained modelling). Physicists then mapped multidimensional space into one-dimensional using the Hilbert curve. This allowed us to maintain correlations between parts of the system.
After that, the researchers compressed the resulting one-dimensional array of numbers without loss using the Lempel-Ziv-Velch algorithm implemented in the 7-Zip program. In short, this algorithm goes along the string of characters and searches for repeating short segments and then replaces them with pointers to the places in which it first encountered such segments. Finally, scientists calculated the degree of compression of the array and mapped it to the entropy of the system. As a first approximation, scientists used a linear function in which the coefficient of proportionality is the number of degrees of freedom multiplied by the logarithm of the number of variables needed to describe each degree of freedom separately. Scientists have proved the validity of this approximation using concrete examples.
To test the proposed method of physics, five systems were considered for which entropy can be calculated analytically. First, scientists have found the entropy of a four-level system at different temperatures. Secondly, physicists considered the two-dimensional Ising model on a square lattice, which described a ferromagnet or a frustrated antiferromagnet. Third, the researchers repeated the calculations for the Ising model on a triangular lattice. Finally, scientists estimated the entropy of a chain of N links, the end and beginning of which are spaced at a fixed distance. In all these cases, the obtained entropy differed from the exact value by only a few percents (not counting the constant shift).
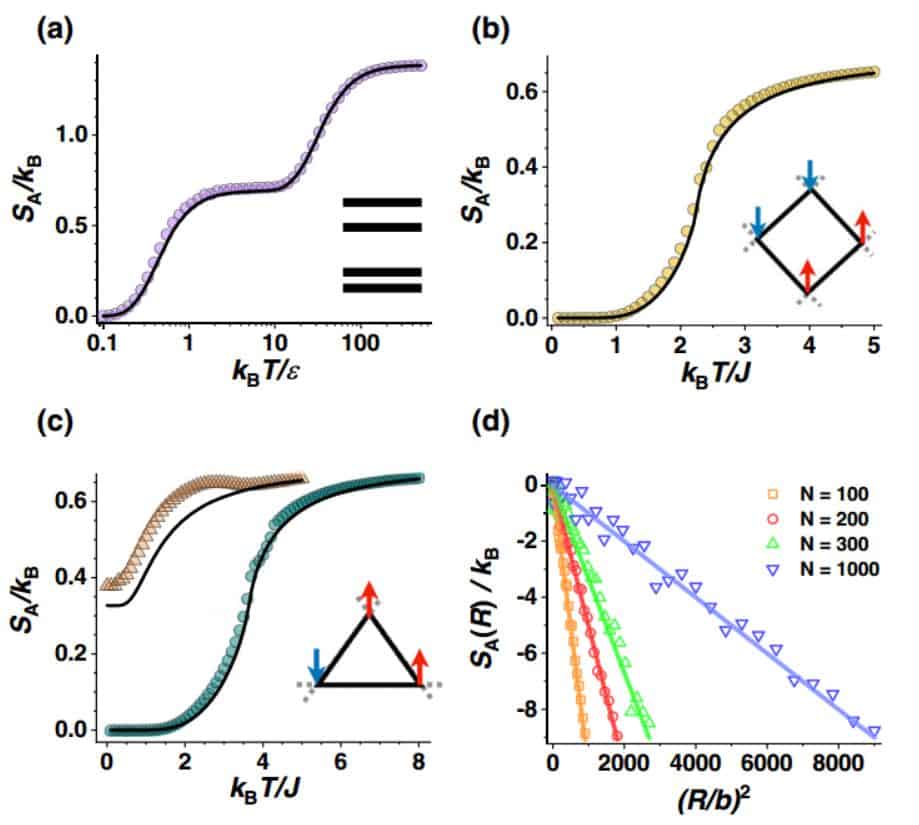
Ram Avinery / Physical Review Letters, 2019
Finally, scientists, inspired by the success of the algorithm on model examples, tried to solve the problem of protein folding (to find out how protein coagulates, you need to find the configuration with the lowest configurational entropy). As an example, physicists considered the C-terminal portion of villin. Using the proposed algorithm, the researchers constructed an h, s-diagram (enthalpy-entropy population diagram), which made it possible to distinguish between collapsed and expanded states with an accuracy of about 95 per cent. Scientists emphasize that to assess the “coagulation” they did not have to use any additional considerations about the structure of the protein.
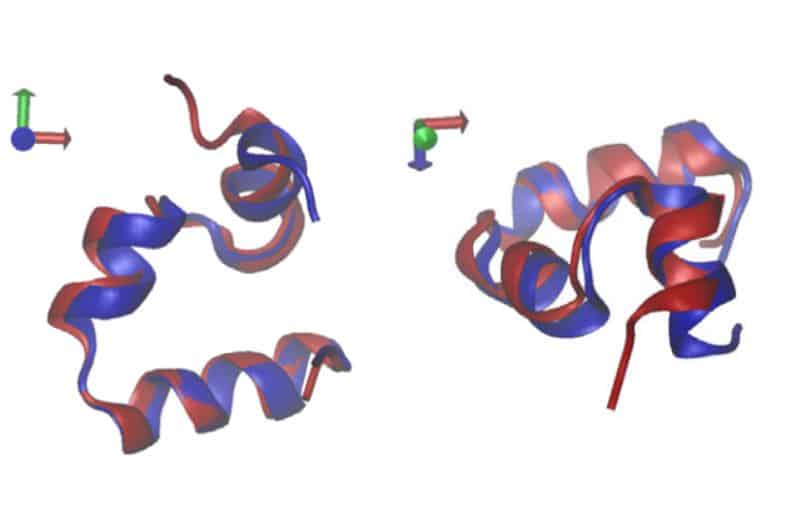
Ram Avinery / Physical Review Letters, 2019
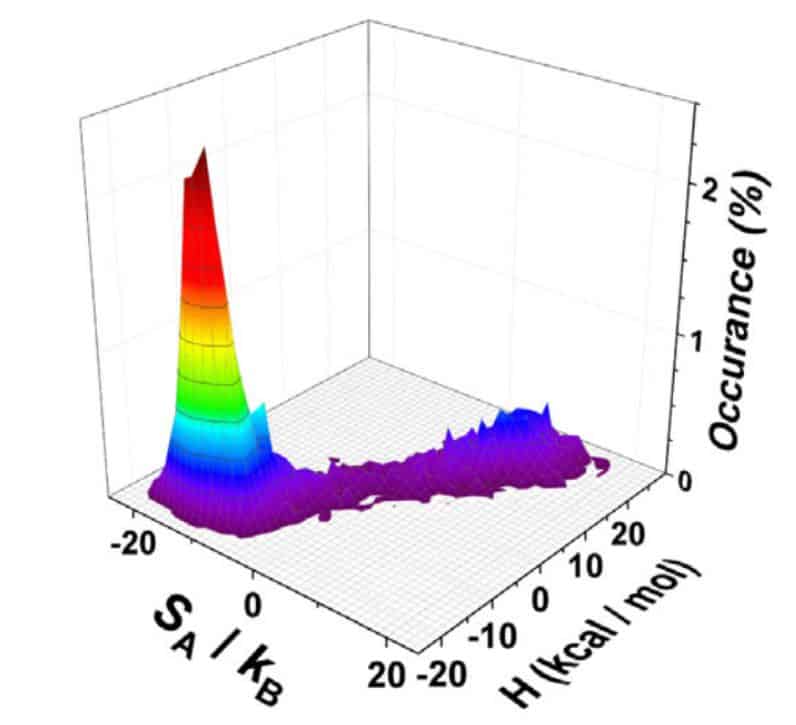
Ram Avinery / Physical Review Letters, 2019
It is interesting that the authors preprinted the article back in September 2017, and sent it to the journal in May 2018. Thus, the article was reviewed for almost a year and a half. However, she was quoted only once during this time.
One unusual example of entropy is entanglement entropy, which is defined as the usual entropy for a “truncated” quantum system. Using this quantity, one can evaluate the degree of quantum entanglement of two systems — for example, particles that are born in the Casimir dynamic effect or are elastically scattered on top of each other. Some physicists even believe that using the entropy of entanglement, one can understand how the quantum states of a black hole are arranged.