On a new research project, Irish researchers have developed and trained a model that predicts the Curie temperature of a ferromagnet, starting only from its chemical composition. At 83 percent, the model is mistaken for less than 100 Kelvin, which allows it to search for promising high-temperature ferromagnetic materials with its help.
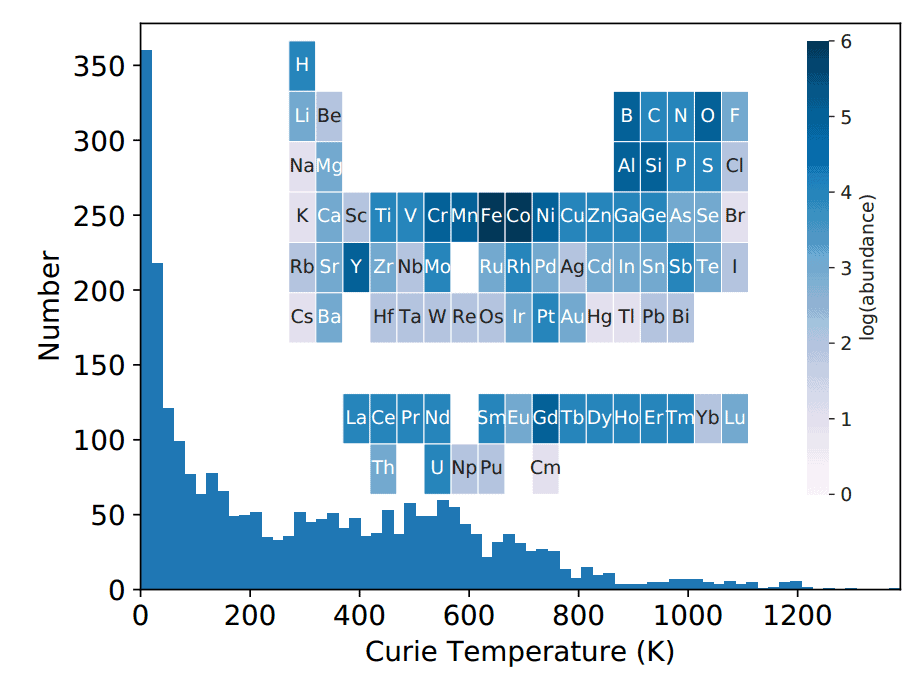
Currently, physicists know more than 2500 ferromagnets, which automatically makes them the most common class of magnetic materials. At the microscopic level, a ferromagnet breaks up into domains – roughly speaking, into small indivisible magnets. If the temperature of the ferromagnet is relatively low, all magnets look in the same direction, their field adds up and amplifies, and as a result the magnetization of the ferromagnet turns out to be large – large enough so that the ferromagnets accidentally detect two and a half thousand years ago. However, as the temperature rises, the magnets begin to “tremble”, their field is no longer so efficient, and the magnetization of the material begins to decline. If the temperature exceeds a certain critical value, the “jitter” will become too strong, and the ferromagnet will be demagnetized. This critical temperature is called the Curie temperature.
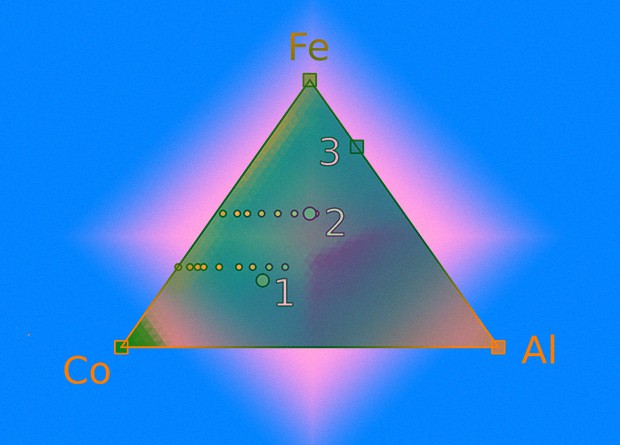
James Nelson & Stefano Sanvito et al. / Physical Review Materals, 2019
Unfortunately, most ferromagnets have a Curie temperature that is too low to be practical. More than half of the known ferromagnetic materials lose their properties at temperatures below room temperature, only a small part of the rich class of ferromagnets survive to “practical” temperatures of more than three hundred degrees Celsius, and only pure cobalt overcomes the mark of a thousand degrees Celsius. Given this fact, physicists continue to search for new high-temperature magnets. Interestingly, the scope for the search is quite large: with the exception of noble gases and radioactive elements, almost every ion from the periodic table can form a ferromagnet if it is placed in a suitable crystal lattice.
Because of this wealth, most searches for new magnets are carried out theoretically using numerical simulations. Unfortunately, the dependencies that link the Curie temperature of a material with its structure and chemical composition are far from obvious. Most of these dependencies are purely empirical. For example, the Curie temperatures of Co 2 XY -type alloys can be described using the Slater-Pauling curve, and the Curie temperatures of similar alloys with manganese follow the Kastelitsa-Kanomat curves. This is due to the fact that standard methods, including a rather powerful theory of the density functional, cannot extract information about the Curie temperature from the structure of the material, although they can calculate its other properties. Therefore, physicists looking for high-temperature magnets still have to follow empirical rules that promising regions may miss. As a result, most of the effort is spent on researching materials with low practical potential.
Researchers James Nelson and Stefano Sanvito partially solved this problem with machine learning. Scientists have developed and trained a model that predicts the Curie temperature of a material, starting from its chemical formula. The prediction error of such a model was about 50 Kelvin. Moreover, the neural network very well extrapolated the scarce source data to new areas.
Since the relationship between the Curie temperature and the chemical composition of a ferromagnet is not entirely clear, physicists have expanded the range of parameters with which the model worked. As a result, scientists received a 129-dimensional vector of parameters. This vector included 84 numbers describing the atomic fraction of each possible element that may be part of a ferromagnet. Since in practice the material consists of one, two, or three elements, for real compounds almost all of these numbers are equal to zero. This indicates that connection information can be stored and calculated more efficiently. Therefore, to these 84 numbers, scientists added 45 more parameters describing the atomic number, group, period, number of valence electrons, molar volume, melting point and electron affinity, averaged over the atoms of the compound, and then “truncated” the vector, highlighting in it only the most important parameters. It is interesting that with proper “truncation” the efficiency of the model remained virtually unchanged – even if only 10 were left from the initial 129 parameters.
Scientists used 2,500 ferromagnets collected from four different sources to train and test the model. Compounds with the same chemical composition but different crystal structure were considered by physicists to be the same material, so the Curie temperature of a “composite” ferromagnet could fluctuate quite significantly. For example, a material with the chemical formula Sm 2 Ni 17 can lose ferromagnetic properties at both 186 and 641 kelvin. To minimize the effect of such fluctuations, scientists assigned median temperatures to “composite” ferromagnets. However, it is worth noting that for most materials the scatter was relatively small: in 80 percent of ferromagnets, the Curie temperature was within an interval of about 50 Kelvin wide, and only in 5 percent the temperature spread exceeded 300 Kelvin.
Since 2500, the sample of ferromagnets was relatively small, the researchers combined training (training) and test (validation) data sets. Recall that on the training data set, the model adjusts the parameters, and on the test data set – hyperparameters, that is, parameters that are set before training begins. To increase the effectiveness of training, researchers tried to select as many different compounds as possible (and even added non-magnetic compounds to them) in these (matching) data sets. The size of the training and test set was 1866 compounds. Using the remaining 767 compounds, physicists tested the effectiveness of the trained model.
As a model of machine learning, scientists used four different algorithms: the Tikhonov regularization method (ridge regression), neural network, random forest (random forest), and ridge core regression(kernel ridge regression). The last two methods performed the predictions best: in 59 percent of the cases, they predicted the Curie temperature with an accuracy of about 50 Kelvin and another 24 percent made a mistake of less than a hundred Kelvin. It is worth noting that the algorithm “broke” only on ferromagnets with a low Curie temperature, which have no practical use. Moreover, the model very well extrapolated the scarce initial data: from just two points, it almost perfectly restored the curves on which the ferromagnetic compounds of various elements lie.
Thus, using the constructed model, it is quite possible to search for new compounds. However, for greater accuracy, it should include data on the structure of the material. In addition, it would be nice to figure out exactly how the model predicts temperature.
Recently, neural networks have become so popular that they are trying to apply them literally wherever possible. Physicists, this mod is also not spared. In particular, physicists have already taught neural networks to count functional integrals and topological invariants, solve the quantum problem of many bodies, correct errors in quantum computers, search for Higgs boson decays, and predict crystal growth. Moreover, some neural networks, no worse than people, “understand” the essence of physical processes in statistical systems, that is, they distinguish degrees of freedom that determine its physical properties.