For the first time, a group of physicists led by Vikram Deshpande from the United States experimentally measured the electronic compression of a one-dimensional Wigner crystal formed in a carbon nanotube. In fact, scientists measured the intensity of interaction between crystal particles. To do this, the researchers tracked the position and magnitude of nanotubes conduit peaks that correspond to the addition of new electrons. According to the scientists, the results are well consistent with the theory of the Wigner crystal.
If the electron gas is sufficiently cooled and destroyed, the electrons will gather in a Wigner crystal, an ordered structure resembling a crystal lattice of an ordinary solid. On the one hand, the low temperature ensures that the electrons are sufficiently “nailed” to the nodes of the crystal lattice – if the kinetic energy of a particle is much less than the potential energy, the amplitude of its oscillations near the equilibrium position is much less than the distance between the nodes. On the other hand, due to the high degree of rarefaction, the probability of particle tunneling between neighboring nodes is small enough so that the crystal does not turn into an electron liquid (the distance between neighboring nodes should be much larger than the Bohr radius) For the first time, the existence of Wigner crystals was theoretically discovered in 1934 by the American physicist Eugene Wigner.
Unfortunately, in practice it was very difficult to obtain such highly correlated systems. The experimenters first made a three-dimensional Wigner crystal in 1979, for a two-dimensional case this method was generalized in 1988, and scientists synthesized a one-dimensional analogue only in the last decade. Of course, the properties of such objects were even more difficult to measure. Just a few months ago, a team of researchers led by Shahal Ilani learned to directly “photograph” the structure of one-dimensional Wigner crystals by measuring the spatial distribution of the charge density of the system. Using the developed technique, scientists directly measured the distance between neighboring nodes of the crystal. The rest of the parameters that control the formation of a one-dimensional Wigner crystal have not yet been measured.
This study experimentally measured another parameter of a Wigner crystal – electronic compressibility. Since the reverse electron compressibility shows how much energy you need to spend to add another electron to the system, in fact, scientists have measured the magnitude of the interaction between the electrons of the crystal. It is worth noting that previously, researchers already tried to measure the reverse compressibility of electronic systems with low temperature and density, but the results of these measurements cannot be unambiguously attributed to Wigner crystals (Deshpande considers these measurements to be insufficiently convincing, because the size of the electronic crystal in them was not kept constant).
To produce a one-dimensional Wigner crystal, scientists used carbon nanotubes – one of the simplest and most convenient one-dimensional systems. Scientists have chosen this system for two reasons. First, several groups independently proved that Wigner crystals actually form in nanotubes, so scientists might not have to spend time checking the resulting structure. Secondly, the effective mass of an electron in a nanotube is proportional to the width of its forbidden zone, which can be adjusted over a wide range using an external magnetic field. This allows to adjust the ratio of kinetic and potential energy – and therefore, to explicitly check how the compressibility is related to the intensity of the interaction.
In practice, scientists made a nanotube using the chemical deposition of the gas phase of hydrocarbons on a substrate in the form of a narrow groove (about two micrometres wide). Depending on the structure of the nanotube, the width of its prohibited zone could vary from 20 to 200 millielectronvolts. The scientists then cooled the system to a temperature of 1.5 kelvins, attached the electrodes to the ends of the tube (source and drain) and the bottom of the groove (shutter). Regulating the voltage between the electrodes, physicists “locked” in the tube electrons, and then estimated their number by the conductivity of the tube (so physicists call the conductivity of one-dimensional systems). To find the inverse compressibility of the system Nof electrons, the researchers recalculated the voltage into energy and added the energy increments during the transition from a system with N particles to systems with N −1 and N + particles (κ −1 = E N + 1 + E N − 1 −2 E N ). Interestingly, in tubes with a narrow bandgap (about 20 electron volts), the reverse conductivity decreased with the addition of new electrons, and in tubes, with a wide bandgap (about 150 electron volts) increased.
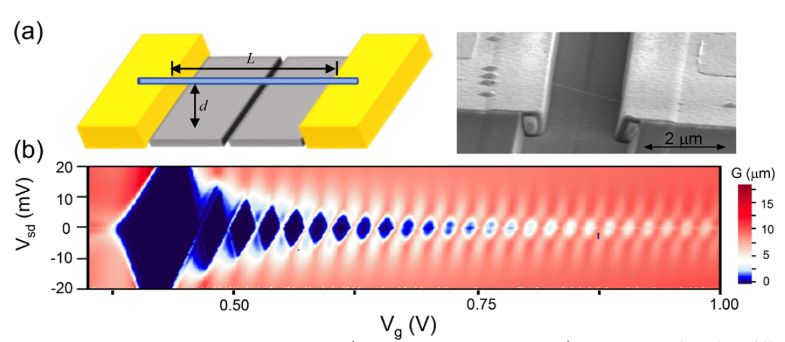
Physical Review Letters, 2019
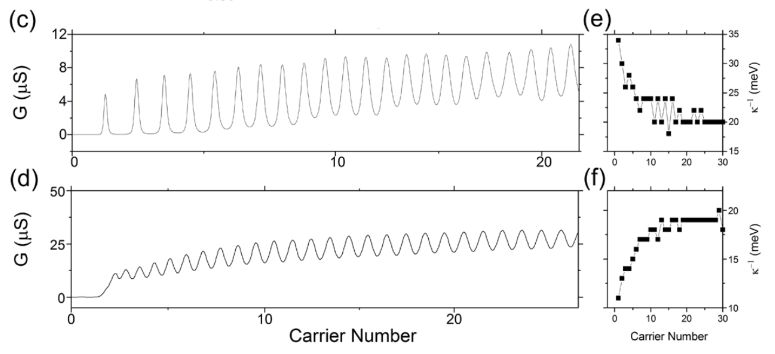
Physical Review Letters, 2019
To more accurately measure how the reusability dependence on the number of electrons looks at different widths of the prohibited zone, the scientists sent along the nanotube axis homogeneous magnetic field. On average, when the magnetic field tension increases by one tesla, the width of the prohibited zone increases by 2.5 millielectronvolts; in the experiment, scientists changed the tension zero to four Tesla. In general, these measurements confirmed the previously discovered dependence: the greater the width of the prohibited zone, the faster the reverse compression (for tubes with a narrow prohibited growth was replaced by a slower decline).
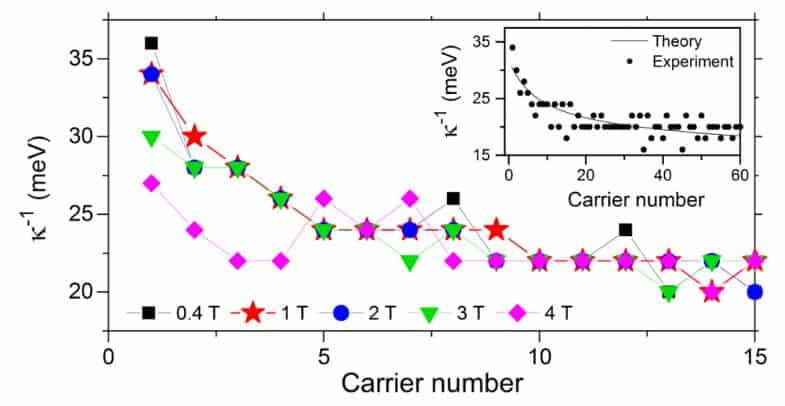
Physical Review Letters, 2019
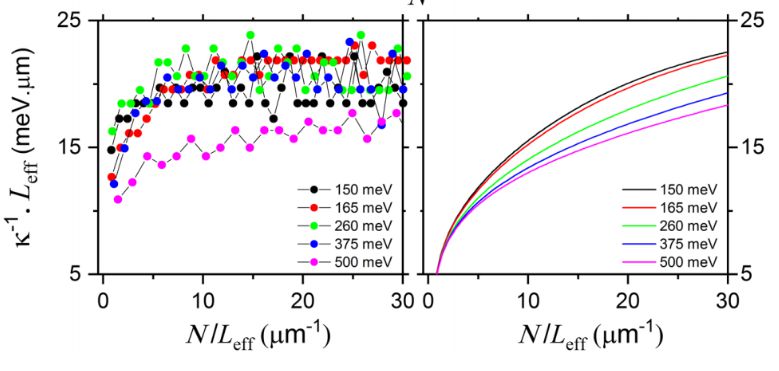
Physical Review Letters, 2019
The scientists explained the results using a high-quality model of the Wigner crystal. Since the kinetic energy of electrons in a Wigner crystal is small compared to the Coulomb repulsion energy, the researchers neglected the overlap of the wave functions of the particles. In this approximation, physicists reproduced the growth that was observed in tubes with a wide forbidden zone. In addition, physicists have taken into account that in tubes with a narrow bandgap (i.e., lighter electrons), the blocking potential that arises is important between the gate and the drain (or source). This potential explains why the reverse compressibility in such tubes increases with a decrease in the number of particles. Scientists do not explain why the blocking potential does not cause the same effects in tubes with heavier electrons. Nonetheless, they believe that the dependencies they obtained are in excellent agreement with the theory of the Wigner crystal.
However, the researchers note that the resulting compression behaviour is not unique to the Wigner crystal – in principle, it can be explained with the same success theory of homogeneous electronic gas with metabolic interaction. However, other experiments that worked with the same systems (in particular, the work of Shahir Ilani’s group) confirm the Wigner crystal hypothesis. Therefore, scientists believe that the measured compression does reflect the intensity of interaction between the particles of the Wigner crystal. In the future, the researchers promise to explicitly test this assumption by combining crystal lattice measurements and compression for the same sample.
When the interaction between electrons is gradually turned off, the one-dimensional Wigner crystal moves into a zigzag structure in which electrons line up in two parallel chains. This effect was first experimentally confirmed last September by physicists from Taiwan and the UK. To do this, the scientists used a nanowire from a semiconductor (GaAs / AlGaAs heterostructure). However, scientists have not yet been able to measure the properties of the zigzag crystal.
