Physicists from ITMO University theoretically predicted the “true” time crystal that exists in continuous time. Until now, it was believed that such crystals could not be created. To circumvent the ban on the creation of such crystals, scientists had to sacrifice the locality of interactions between parts of the system – roughly speaking, the proposed by a time crystal you can only create a system in which each atom is directly connected to all other atoms (not just the nearest neighbors). However, the lack of locality does not mean that the proposed model cannot be implemented in practice.
Physicists call crystals systems, which are periodic in space and retain their structure at relatively weak perturbations. In other words, such a system only translates into itself with certain discrete transformations, which are reduced to translations (shifts) to a fixed vector. For example, a simple cube lattice is stored when shifts to vectors built from three perpendicular vectors of the same length. Most known crystals are made up of atoms, but the definition of a crystal can be easily extended to other systems with discrete spatial symmetry. In particular, scientists have already learned how to create crystals from photons and bulk materials.
In addition, the definition of a crystal can be naturally summarized into a four-dimensional space, requiring the system to have additional invariance in time translations. This was first proposed by Nobel laureate Frank Wilczek in 2012. Unfortunately, a few years later, Japanese researchers Haruki Watanabe and Masaki Oshikawa showed that in practice space-time crystals cannot be created: if the system gets into a state with the least possible energy, it is in it for an indefinite time, and if it comes out of the minimum, it loses the periodicity in time.
However, loopholes remained in the proposed evidence. First, it suggested that the evolution of the system is stationary. Secondly, the scientists limited themselves to considering the close-up particles, the potential of which is gradually reduced with distance. Subsequently, the first loophole allowed the creation of so-called “crystals in discrete time” – systems that periodically “push” external influences and which are invariant with respect to broadcasts over a gap several times longer than the exposure period. The second loophole has not been used by scientists so far. At the same time, it potentially allows you to get full crystals that break the symmetry of continuous-time rather than discrete, but in the same way, as ordinary crystals violate the symmetry of continuous space.
Physicists Valerii K. Kozin and Oleksandr Kyriienko used this loophole and for the first time offered a model of crystal in continuous time. To test that the constructed Hamiltonian indeed describes a time crystal, the scientists used the strict definition proposed by Watanabe and Oshikawa. According to this definition, a time crystal is a system in which a correlation function from two operators that meets the parameters of an order and is taken at different intervals time, the thermodynamic limit tends to periodic function. In fact, this definition is equivalent to the assertion that a time crystal consists of a large number of subsystems, and its structure is periodically repeated over time. As subsystems, scientists have chosen quantum states of a set of qubits, and as a parameter of order – the total magnetic moment of the system along a given axis.
At first, the researchers tried to construct the Hamiltonian of the time crystal in the most general form. For this, physicists have chosen the ground state |E0 ⟩ fixed energy and then use the operator the total magnetic moment of it built support state | E 1 ⟩∝M̂ z | E0 ⟩. The remaining N −2 states were determined by scientists in such a way that they are orthogonal to the first two.
It turned out that in a system collected from such states, the condition of the existence of a temporary crystal is reduced to two simple conditions. On the one hand, in the limit of a large number of states, the average value of a system’s magnetic moment square should be more than zero. On the other hand, the value of the magnetic moment in the main state should be zero for the arbitrary size of the system. If both of these conditions are met, the required correlation function is periodic, and the system describes the time crystal. For reliability, the scientists also tested that the resulting structure is stable relative to weak disturbances, and summarized the calculations in case of finite temperature.
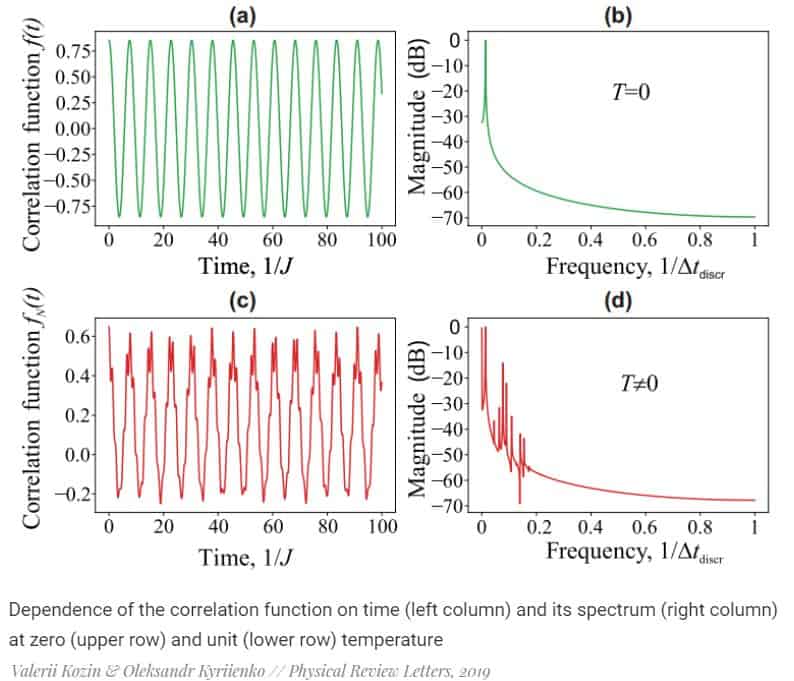
An example of a ground state that satisfies the required conditions is the Greenberger – Horne – Zeilinger (GHZ states) state — a superposition of states in which all spins are directed up and down. In principle, such a state (as well as orthogonal states with higher energy that supplements it) can be completely realized using a system of qubits.
It is important to note that the Hamiltonian corresponding to the constructed time crystal turned out to be strongly nonlocal. If we rewrite it in terms of interactions between individual qubits, it turns out that each qubit directly affects at least half of the remaining qubits (scientists have proved that a less nonlocal Hamiltonian cannot respond to a time crystal). In other words, any excitation instantly covers the entire system described. In a sense, nonlocality is a necessary fee for breaking continuous symmetry with respect to arbitrary translations in time. However, this condition does not mean that the proposed idea cannot be implemented in practice – in principle, now physicists are already able to build nonlocal qubit systems.
One of the first crystals in discrete-time was built in 2016 by a group of physicists led by Christopher Monroe. The basis for the crystal was a nonequilibrium system of several cooled atoms. And in October 2018, researchers from the Netherlands first created a “space-time crystal” in the Bose condensate of cold sodium atoms trapped in an optical trap. Such crystals are simultaneously periodic in discrete time and in space.
