Researchers from the United States theoretically estimated the cross-section and the probability of the creation of miniature black holes in the collision of two electrons. It turned out that despite the increase in the gravitational interaction at an energy of one hundred gigaelectronvolts, black holes are born with an insignificant probability of about 10 ⁻¹³ and a tiny cross-section of the order of 10 ⁻⁴⁵ square centimetres. This is a trillion times less than a naive geometric estimate. Moreover, as the collision energy increases, the cross-section for the production of black holes remains constant.

The hoop conjecture claims that a collision of two high-energy particles can give rise to a miniature black hole – for this, it is necessary that at some point the particles are less than the Schwarzschild radius calculated for the collision energy in the centre of inertia system. To find the cross-section of such a process, it is necessary to design the event horizon on a plane perpendicular to the line of the collision of particles and calculate the projection area. In this sense, the birth of a black hole is no different from a simple example with two billiard balls. However, at the birth of black holes, one must take into account that the gravitational radius is proportional to the collision energy and the gravitational constant – therefore, with an increase in these parameters, the “target” becomes larger, and with it the probability of getting a black hole grows.

Of course, with the standard value of the gravitational constant, the probability of such a process is negligible. For example, for a stationary electron (mass about 9.1 × 10 ⁻²⁸  grams), the Schwarzschild radius is approximately 1.3 × 10 ⁻⁵⁵ centimetres. Nevertheless, some theories suggest that at energies of the order of 250 gigaelectronvolts, the value of the gravitational constant increases sharply. This is due to the fact that at such energies the Higgs boson joins the graviton, which can also be considered a particle-carrier of gravitational interaction. In fact, for both the graviton and the Higgs boson, the coupling constant with a particle (fermion) is proportional to the mass of the particle. Therefore, the Higgs virtual boson exchange describes an interaction similar to the virtual graviton exchange. In the general case, this interaction is described by the theory of scalar-tensor gravity, built-in 1961 by Karl Brans and Robert Dicke.

However, there is an important difference between the graviton and the Higgs boson: while the graviton has practically no mass, the boson “weighs” about 126 gigaelectronvolts. This means that the long-range potential of Newton turns into a short-range potential of Yukawa, which exponentially decays at distances of more than 10 ⁻¹⁵ centimeters ( Compton wavelength of the Higgs boson). At the same time, at lower distances, the potential generated by the scalar gravity more than 30 orders of magnitude greater than Newton’s habitual potential. The gravitational radius of black holes also increases by the same amount. The cross-section for the production of black holes, calculated using the adjusted radius, is quite noticeable: for example, for the collision of electrons with an energy of 100 Giga electron-volts each section of this process is approximately 3.2 × 10 ⁻³³ square centimetres. However, in practice, such a naive estimate can turn out to be overestimated, since it does not take into account the interaction of particles.

Physicists Han Qi and Roberto Onofrio corrected this naive estimate by considering the interaction of two electrons in the Standard Model. Given that the main contribution to the interaction of two electrons is made by the Coulomb repulsion, physicists have considered a very simplified collision model. First, scientists neglected the spin of the particles, that is, they replaced the usual gauge electrodynamics with scalar electrodynamics. Secondly, the researchers neglected the magnetic field: although such a field is generated by flying charged particles, it is many times smaller than a static electric field. Third, physicists neglected relativistic effects; in other words, scientists considered the interaction of two resting electrons, but attributed to them the “right” energy, in γ times the resting energy. Finally, the researchers neglected the change in the black hole metric associated with electromagnetic interaction, since for an energy of more than 30 gigaelectronvolts such changes are negligible.

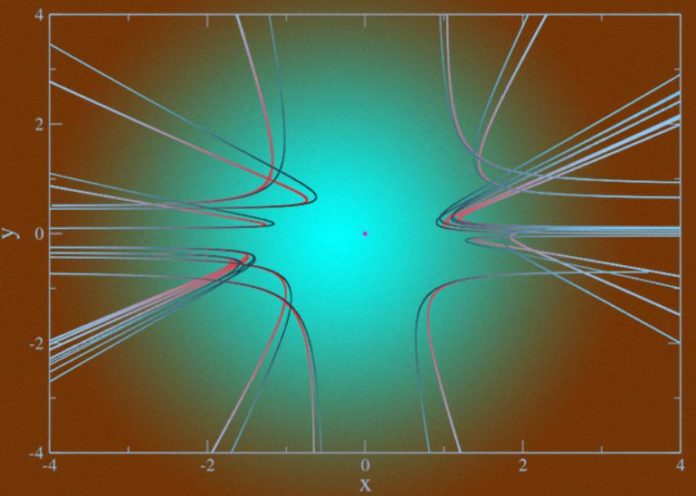
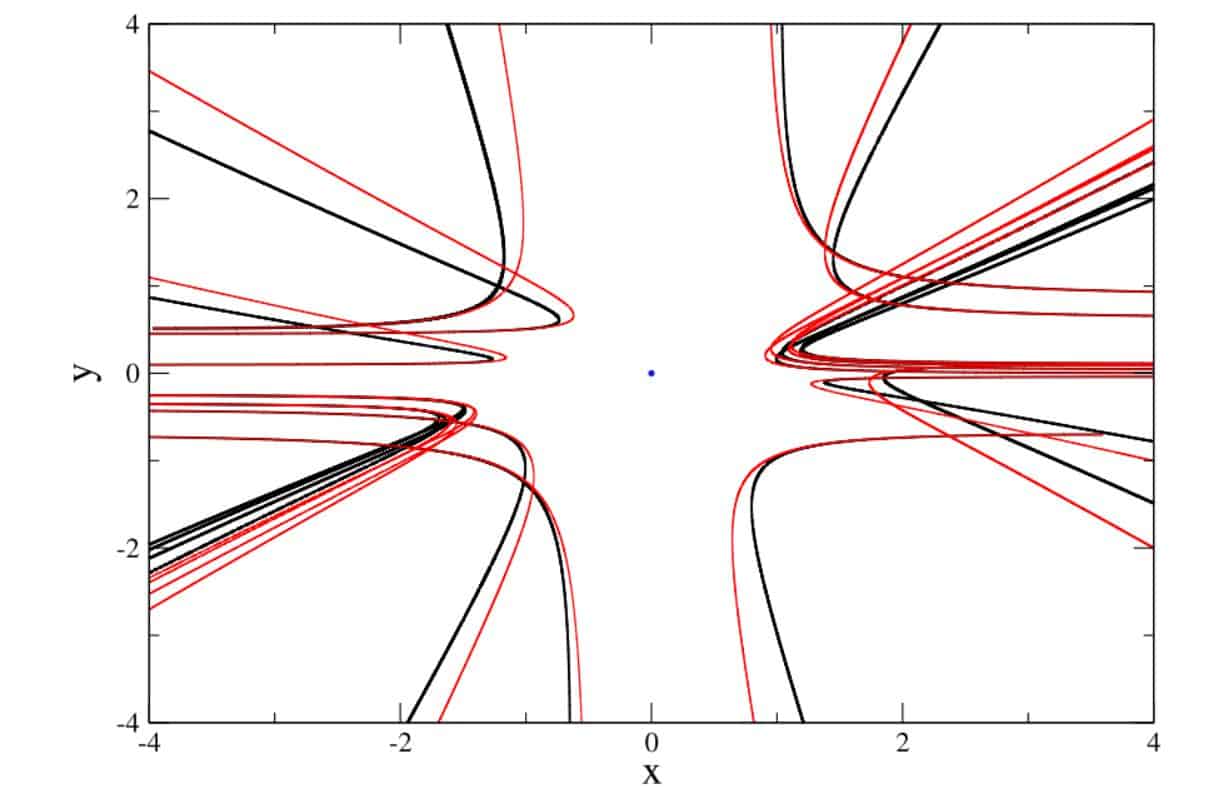
To model particle interactions, scientists relied on two fundamentally different approaches. In the first approach, physicists numerically integrated the two-dimensional Schrödinger equation, which corresponds to a particle with reduced mass placed in the effective (Coulomb + Newton + Yukawa) potential. Using the cylindrical symmetry of the collision, scientists “squeezed” three-dimensional space to two-dimensional space. Solving this equation, scientists found the wave functions of the particles and checked the probability with which the particles are less than the Schwarzschild radius.

The second approach was based on extended Gaussian dynamics – the semiclassical method proposed by Poole Ehrenfest in 1927. This method works with averaged momentum and particle coordinates, as well as with an effective potential expanded in averaged degrees of the coordinate. Generally speaking, all these averaged variables obey the infinite Heisenberg system of equations, but it can be “reduced” to four equations, assuming that the wave functions of the particles are Gaussian. By solving these equations, the probability of the formation of a black hole can be calculated analytically, although approximately.

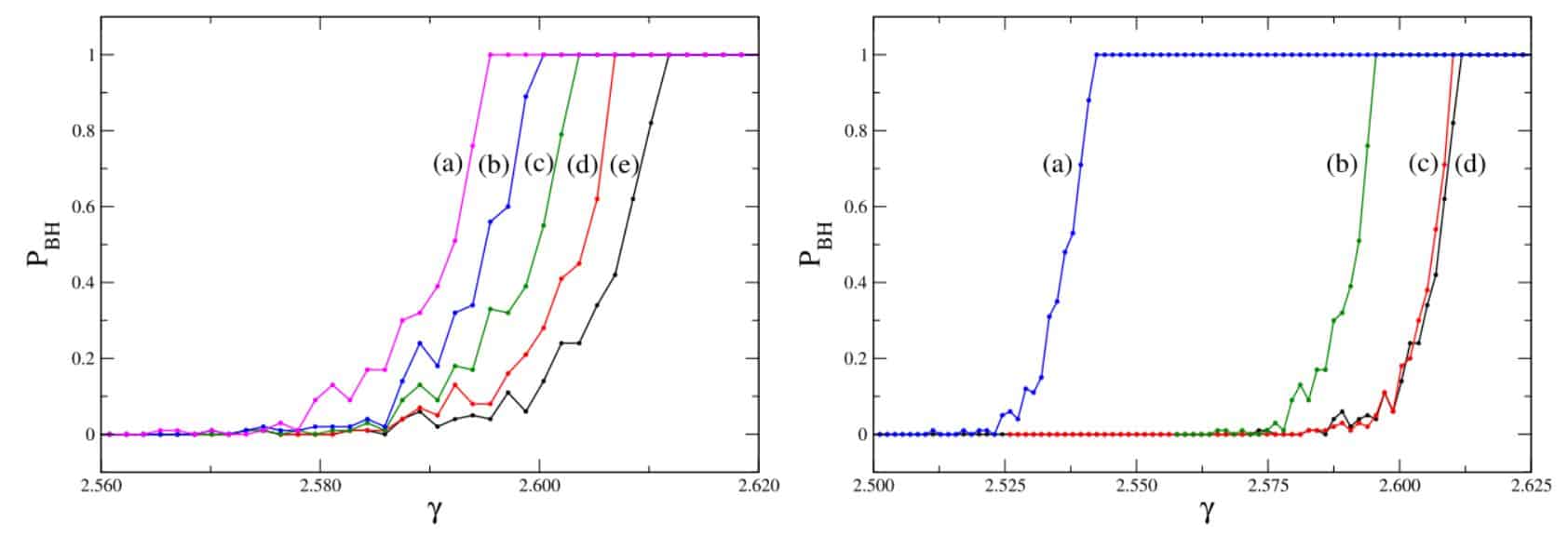
As expected, scientists have found that when electrons converge, the distance is less than the Schwarzschild radius, the probability of black hole production jumps sharply from zero to unity. In addition, the scalar potential affects the scattering of particles in other cases, “softening” their repulsion. However, the main result of scientists is the cross-section of the birth of black holes, which turned out to be almost a trillion times less than the naive estimate. This difference is due to the fact that processes in which particles pass at a fairly close distance make up only a small fraction of all kinds of collisions with a given energy. For example, at an energy of 100 gigaelectronvolts, the probability of a black hole is born with a probability of only 7 × 10 ⁻¹⁴, and the cross-section of the corresponding process is 5 × 10 ⁻⁴⁵square centimetres. Moreover, with increasing energy, this cross-section remains constant, although against the background of other processes the birth of black holes appears more and more clearly.

It is worth noting that even those black holes that can hypothetically be synthesized at colliders are not dangerous: instead of absorbing surrounding matter, they evaporate almost instantly due to Hawking radiation. This is due to the fact that with decreasing hole size, the radiation power only increases. In addition, Hawking radiation does not allow small black holes to trigger the decay of a false vacuum – another process that could theoretically destroy the Earth (and then the rest of the Universe).