Scientists have used deep learning of neural networks to predict the outcome of the gravitational interaction of three bodies. The proven methodology turned out to be faster than traditional solutions up to 100 million times. To begin with, the researchers have limited the space of initial parameters, but they plan to study the problem in the general case.
The task of three bodies is to search for the coordinates and velocities of three material points at an arbitrary point in time under given initial conditions and only gravitational interaction is taken into account. This problem was described by Isaac Newton at the end of the XVII century, but, despite the simplicity of the formulation, this task is extremely difficult to solve due to the manifestation of chaotic dynamics.
Usually they discuss the so-called limited three-body problem, when the initial parameters make it possible to neglect some effects. For example, if the mass of one of the bodies is much smaller than that of the others, then the attraction of large bodies to the lung can be equated to zero – in this case, the movement of bodies in the future can be analytically calculated.
There is a solution to the three-body problem in the general case, found by the Finnish scientist Karl Sundman, but it is of little practical use, as it is expressed as a series with very slow convergence. Due to the properties of this solution, to obtain an answer with acceptable accuracy, it is necessary to summarize too many terms, which even modern computers cannot do.
As a result, in fact, the only solution method used is numerical integration, that is, an iterative solution to the problem in the form of a sequence of small displacements of bodies. However, this method is also very resource-intensive for calculations with high accuracy, and the total amount of time required to receive a response is not known in advance.
From a practical point of view, the three-body task was of historical importance for navigation until the middle of the 19th century – before the appearance of sufficiently accurate ship chronometers, longitude was often determined by the displacement of the moon, but for this it was necessary to calculate its position in the future. Today, solving this problem would help to estimate the likelihood of close passages in areas with a high concentration of astronomical objects, such as galactic nuclei and globular clusters.
The work of astronomers from the UK, Portugal and the Netherlands with the participation of Philip Breen from the University of Edinburgh describes a new method for finding solutions to the three-body problem using neural networks. Scientists trained the program using the deep learning method, but to begin with they limited the space of initial parameters. As a result, the neural network was able to predict the positions of bodies over a time of the order of a millisecond, while modern numerical Brutus algorithm spent, as a rule, 10 thousand times more time, and sometimes lagged 10 million times.
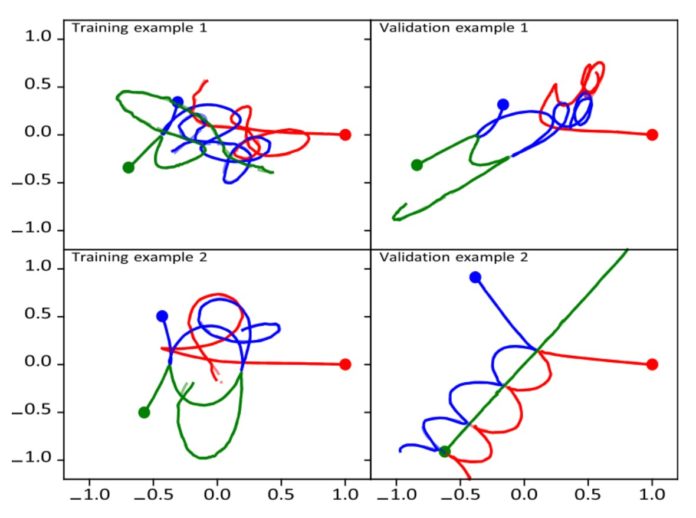
The training sample was formed from the solution of the problem by the Brutus algorithm. Only the initial conditions with three bodies of equal masses, a symmetric arrangement, and zero initial velocities were considered. In this case, the trajectories of the objects will lie in one plane, the number of initial parameters is reduced to two, and the positions of the bodies at subsequent times can be described by three numbers. The training sample consisted of 9900 simulations, and the test sample consisted of 100.
Scientists used a feed-forward ANN multilayer neural network with 10 hidden layers and 128 nodes. The loss function, for which researchers used the average absolute error, turned out to be less than 0.1. Researchers also additionally tested the operation of the neural network for 5000 new simulations, which were distinguished by a small change in the initial parameters, in which the program showed sensitivity to the initial coordinates, that is, it correctly reflected the chaotic dynamics of the system.
An additional test of the work of the neural network was the estimation of the energy of the movement of bodies. In the initial version, the accuracy was low: as a rule, it was at the level of 10 -2, but with close passages it could increase to 10. Nevertheless, the use of an additional neural network, trained to evaluate only the speed of bodies, allowed to reduce the energy error to 10 –5.
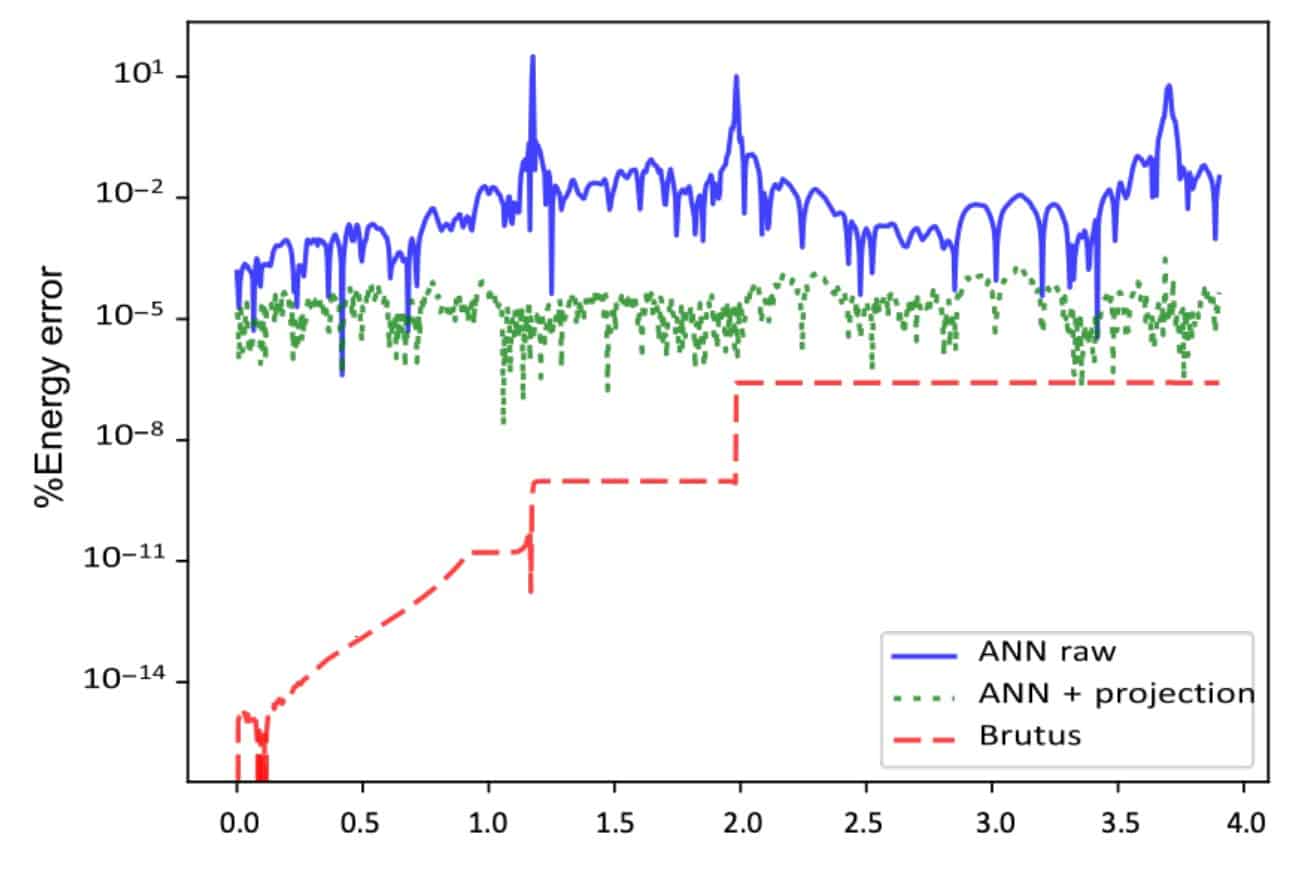
Scientists note that the results show the potential of neural networks in solving the three-body problem. Nevertheless, they do not propose to completely abandon numerical integration, but use a hybrid approach in which the neural network will be used only for situations difficult for traditional methods. Scientists also note that it is necessary to conduct training on a wider sample, including the largest possible amount of parameter space. Moreover, they hope in the future to apply this approach to solve even more labor-intensive tasks of four and five bodies.