French physicists have explained why the end of a closed spinning chain rises spontaneously: it turned out that this effect occurs due to drag. In addition, scientists investigated the formation of waves in such a chain and proposed to measure the tension force with their help. According to the researchers, the results can be useful in practice – for example, when calculating the movement of the aircraft refueling hose.
Although a suspended chain (or a rope, which is one and the same in some approximation) seems like a very simple object, in reality, many interesting effects are associated with it. Probably the most unusual of them is the so-called “chain fountain” : if you fold the chain into a glass and pull out the free end, it will bend in an arc and maintain its acquired shape until it completely “spills” out of the glass. In fact, folding a chain into a glass is not even necessary, you can simply lay it out on a plane. In addition, scientists often investigate how a chain rolls off a smooth surface – it turns out that in some cases this movement also occurs in a paradoxical way. For example, if the rolling chain was originally folded in half, then at some point the acceleration of the folded section will exceed the acceleration of gravity.
Moreover, some modern technologies rely on the movement of thin and flexible objects, in fact the very same chains immersed in a liquid or gas. In particular, an ultrasonic rangefinder with which the ship controls the depth of the bottom and a hose with which the aircraft can be refueled in the air have this shape. The movement of such an object is determined by the ratio between the forces of gravitational attraction, resistance of the medium, cable tension and bending stresses. In the general case, it is rather difficult to theoretically calculate the behavior of a chain placed in such conditions.
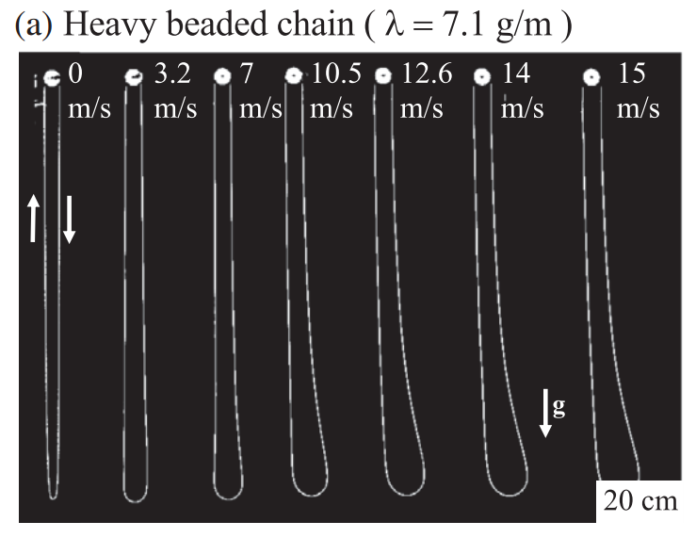
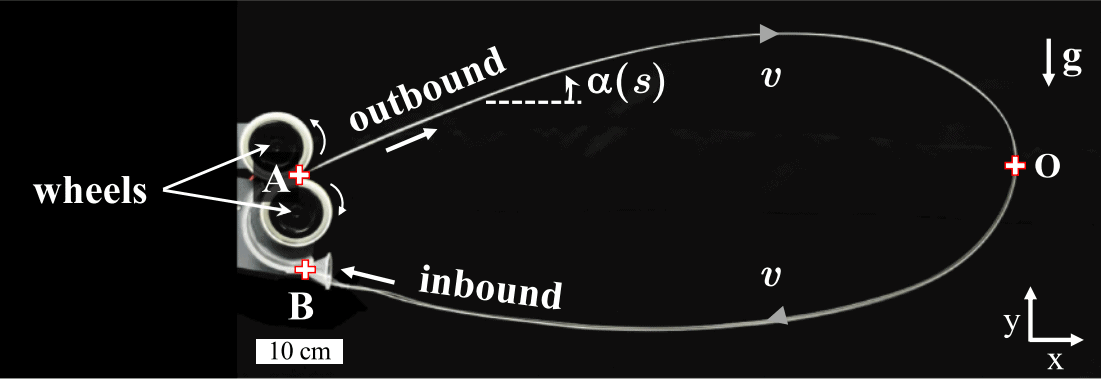
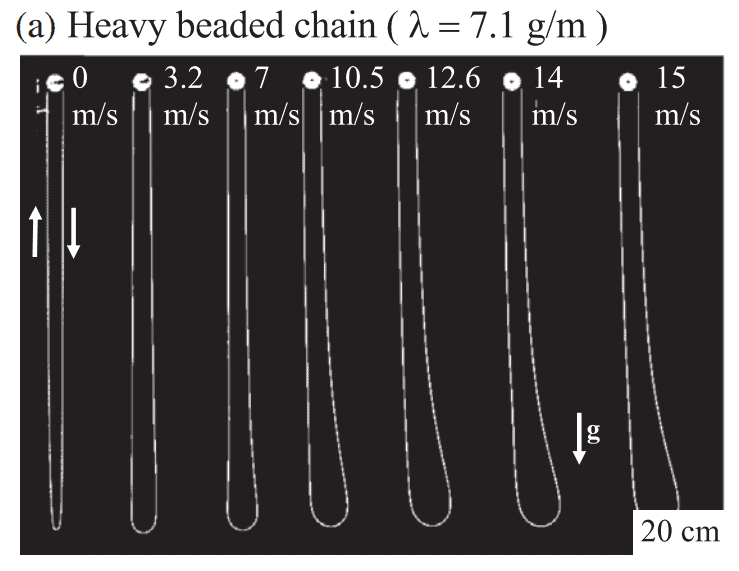
Therefore, a group of physicists led by Nicolas Plihon experimentally investigated the motion of a chain in the air, and grasped a few general patterns that govern it. To simplify the problem, scientists considered the movement of a closed chain, sandwiched between rotating wheels and accelerated to a constant speed v (since the chain was almost inextensible, the modulus of speed of all its points coincided). As a chain, scientists chose heavy beads or a light cotton lace. Since the chain does not leave the vertical plane during movement, its shape can be described by setting the angle between the infinitesimal element of the chain and the horizontal at each point. In this case, it is natural to select the point at which the chain rotates at an angle of 90 degrees to the horizontal (point O in the figure), and select the outgoing (curve AO) and incoming (curve OB) parts in it.
Nicolas Taberlet et al. / Physical Review Letters, 2019
Obviously, three forces control the movement of the chain — the weight of the chain pulling it down, the tension force directed along the chain, and the drag against the movement of the chain. Scientists emphasize that due to the symmetry of the task, the lifting force can be neglected. The researchers also note that it is convenient to divide the chain tension into the kinetic contribution associated with the motion, and the effective contribution that complements it to full tension. Using these notations, the equations of motion can be reduced to dimensionless quantities, which are much more convenient to work with.
Depending on the relationship between two external forces — gravity and resistance — physicists have identified two fundamentally different situations. In the first case, when the force of air resistance could be neglected, the lace profile was practically independent of speed and reduced to an ordinary chain line. The only difference between this case and the static one was that the chain line tension was shifted by kinetic tension.
Nicolas Taberlet et al. / Physical Review Letters, 2019
In the second case, the behavior of the lace was counter intuitive: despite the lack of lifting force, the end of the chain began to rise, and the more noticeable, the higher its speed. According to scientists, this behavior can be explained by air resistance, which is directed upwards on the right side of the chain, vertically falling down. Firstly, this assumption is consistent with analytical and numerical calculations. Secondly, the effect completely disappears when air is pumped out of the chamber.
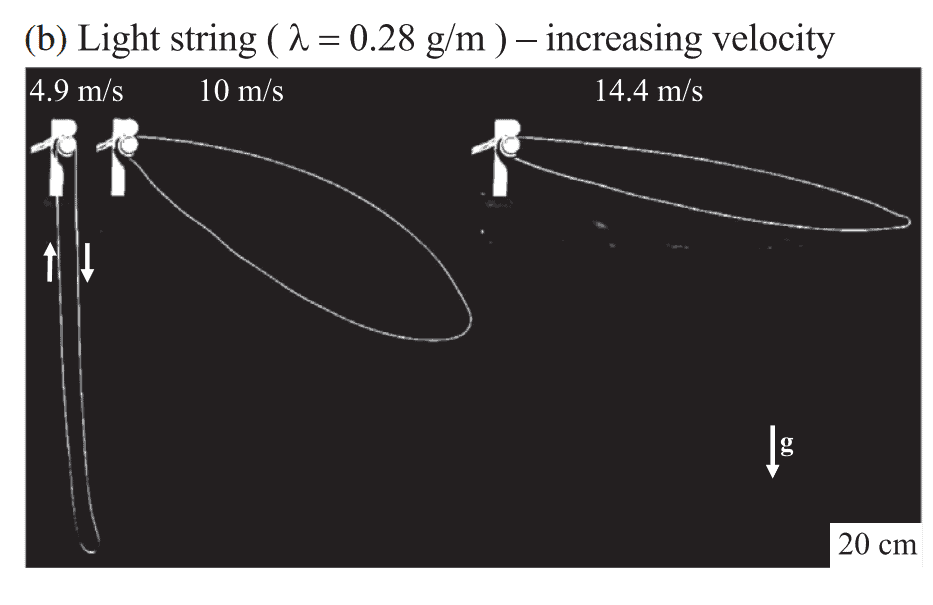
In addition, physicists found that due to the heterogeneity of the chain (for example, a knot tied to a lace), waves moving with a variable speed c ( s ) ≈ ( T( s ) / λ) ½ , where T ( s ) Is the total tension of the chain, λ is its linear mass, and s is the coordinate along the chain. In the case where the chain tension was slightly different from the kinetic tension, the wave velocity practically coincided with the chain speed, therefore, for an external observer, they looked like “slow” waves (moving along the curve with speed v – c ) and “fast” waves (with speed v+ c ). However, the “fast” waves quickly reached the edge of the chain and reflected, turning into “slow” ones. It is interesting that the speed of the waves can uniquely restore the chain tension at all its points. The authors suggest that this remark may come in handy when working with real “chains” – hoses and ropes.
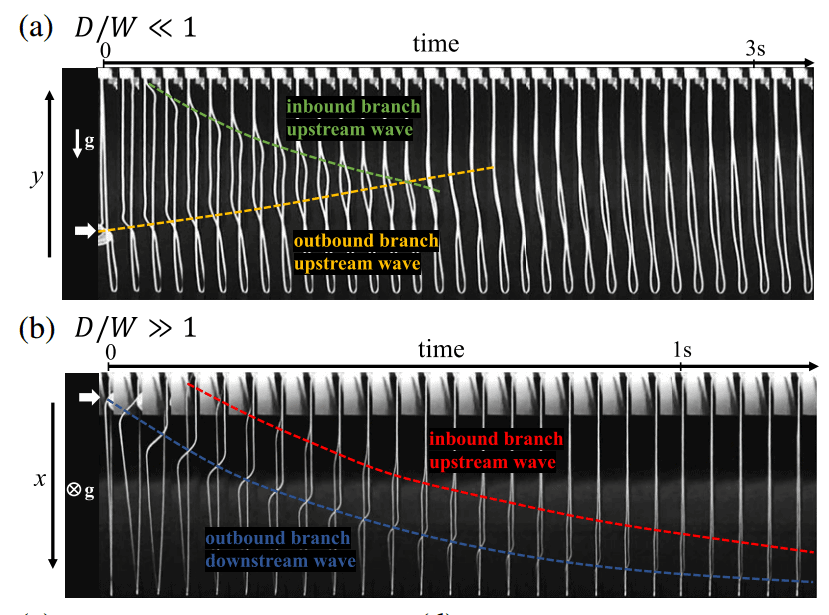
Nicolas Taberlet et al. / Physical Review Letters, 2019
Generally speaking, aerodynamic properties are often manifested even in unexpectedly simple effects. For example, in September 2015, physicists from the University of California and the Sharif University of Technology (Iran) found that a twisted ring lying on a table tends to return to its original position, like a boomerang. At the same time, a coin placed in the same conditions does not possess such properties. Scientists attributed this effect to the fact that a small layer of “locked” air separates the coin from the surface, while the ring does not have such a layer. This increases the friction force and at some point causes the ring to turn back.
Source | Physical Review Letters