Physicists from Sweden and China for the first time directly measured the wave function of states separated in space – the polarizations of two entangled photons. For this, scientists modified the method of weak measurements, replacing weak values with modular ones. Previously, it was possible to measure the wave function of such states only with the help of quantum tomography.
As a rule, to measure the wave function of a system, physicists use quantum tomography – they make and measure many copies of the system, and then restore the expansion coefficients of the wave function from basic states. It is important that the measurements be carried out in different bases – otherwise the information on the phase of the wave function will be lost, and only the probability density (i.e. the square of the wave function) will be obtained from the results obtained. Both of these complications are related to the uncertainty principle. Heisenberg, which relates the uncertainties of two additional observables (that is, observables whose operators do not commute). The simplest example of such observables is coordinate and momentum. If we try to accurately measure the position of the particle, then we will involuntarily “push” the particle and increase the uncertainty of its momentum. Thus, the wave function of the particle after measurement will change in an unpredictable way, and it will be impossible to get information about the initial state.
However, quantum tomography is not the only way to circumvent the limitations of quantum mechanics and measure the wave function of a system. The alternative is the method of weak measurement, developed by in 1988 by Yakir Aaronov, David Albert and Lev Weidman. Roughly speaking, in this method, the measuring device very weakly excites the system, extracting a small amount of information about its state. The result obtained from such a measurement is called the “weak value” of some observable. To enhance this effect without destroying the quantum state of the system, physicists in a special way “sift” the initial and final states obtained in multiple realizations of the process. It is important to note that weak measurements make it possible to directly obtain information about the wave function, bypassing the reconstruction stage from quantum tomography.
In practice, the method of weak measurements was first implemented in 2011 by a group of physicists led by Jeff Lundeen, who determined with its help the wave function of an individual photon. A few years later, the same group extended the method to a system of two quantum states – orthogonal polarizations of one photon.
However, the weak measurement method has one significant drawback: the states of the measured system cannot be separated in space. This is due to the fact that for the standard implementation of the method, all states should be perturbed at the same time. To realize such instant long-range action in practice is impossible. In principle, this drawback can be circumvented with the help of multiple weak measurements, however, using this method, complete information about the system cannot be obtained. Therefore, to measure the wave function of such systems, one has to return to quantum tomography.
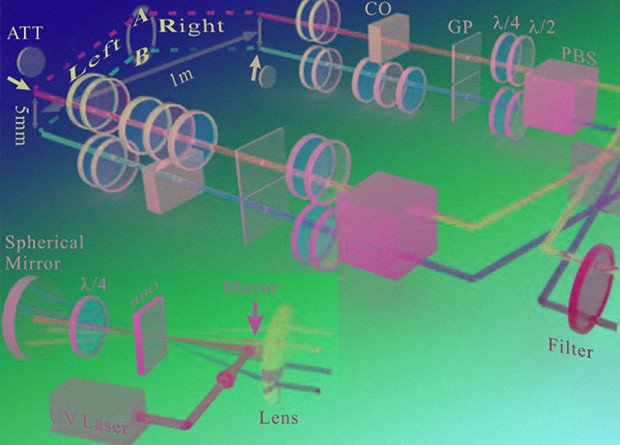
A group of physicists led by Guang-Can Guo extended the weak measurement method to systems with spatially separated states, replacing the weak values of the observables with modular values. To obtain such a value, it is necessary to project on the initial and “sifted” state not the operator itself, corresponding to the observed value, but some function of it. Scientists also applied this method to two entangled photons – thus, for the first time, researchers directly measured the wave function of two entangled states separated in space.
To generate entangled photons, scientists shone an ultraviolet laser on a barium beta-borate crystal, which turned individual photons into photon pairs with confusing polarization and momentum. Then the scientists measured the modular value and restored the wave function of entangled polarizations, using as the “entangled meter” the paths along which the photons went through the setup. Roughly speaking, in this method, the probability of detecting a “counter” in a certain state is uniquely related to the real and imaginary part of the modular values of the projection operators on the state with a given polarization of each photon, and the modular values are uniquely related to the wave function of entangled states. Scientists used a Francon interferometer to measure probabilities, and the polarization of the photons was controlled using polarizing plates. As a result, scientists obtained the wave function of entangled polarizations, which is in good agreement with tomographic measurements.
Every year, physicists manage to measure the properties of wave functions of more and more complex systems. For example, in October 2017, researchers from Austria and Germany learned to register a change in the phase of the wave function of a two-particle system corresponding to a permutation of particles. In January 2018, another group of physicists first measured the square wave function of an electron in a hydrogen molecule. To do this, scientists destroyed the molecule using a high-energy light beam, trapped the resulting decay products and restored the correlation functions from these data. And in July 2019, Scottish physicists first “photographed” entangled photons at the time of the uncertainty of their physical conditions.
Via | Physical Review Letters and reports