Researchers from China and the United States appreciated how objects located on opposite sides of the wormhole interact. It turned out that due to the “gluing” of the fields at the border of “our” and “other” spaces, observers feel the electric, scalar and gravitational fields of objects from the opposite edge of the hole. According to scientists, with the help of the effects found, it can be checked whether the object Sgr A * in the center of the Milky Way is a wormhole.
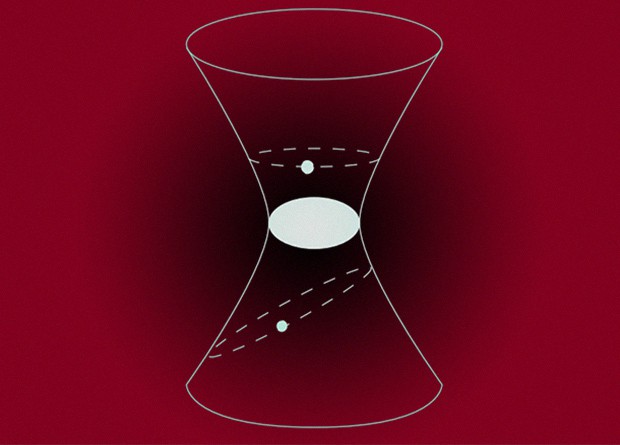
Physicists divide wormholes into passable and impassable. An impenetrable wormhole is destroyed faster than an object that has got into it manages to exit from the opposite end, therefore, it looks almost the same as an ordinary black hole. Passable wormhole can potentially connect different areas of space-time. In particular, a stream of a field created by objects on opposite sides of a hole can pass through such a hole – therefore, objects will feel each other long before falling into the hole. In particular, if the field of objects changes in time, the observer will understand that the field measured by him cannot be created by a static black hole, and he will guess that he is working with a passable wormhole.
Physicists De-Chang Dai and Dejan Stojkovic turned these qualitative considerations into formulas and appreciated how objects located on opposite sides of the wormhole to pass will interact. To do this, scientists considered a simplified model of a wormhole — two flat three-dimensional spaces continuously glued along a spherical inner boundary. Such a model completely ignores the nature of the wormhole and the processes occurring inside it, but physicists believe that these details almost do not play a role for an external observer. At the same time, due to the simplicity of the model, the results obtained in it can be easily interpreted.
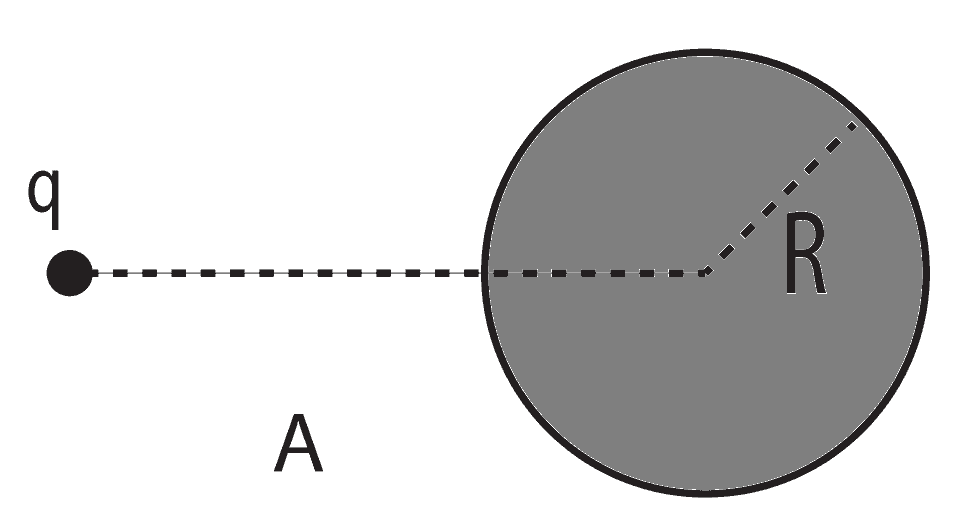
In order to qualitatively evaluate the effects of the “tunneling” of fields, physicists first considered a point electric charge q located at a fixed distance A from the wormhole. Near the charge, the electric field is described by the usual Coulomb law, however, as it approaches the boundary, it begins to distort. Given the spherical symmetry of the border of the wormhole, physicists expanded the amendments to the Coulomb law in a series, each member of which gradually fell away from the hole. Demanding that the field potential and the derivative along the radial direction be continuously glued at the boundary of spaces, physicists found the expansion coefficients in the charge space (“another” space) and the space at the opposite end of the hole (“our” space).
De-Chang Dai & Dejan Stojkovic / Physical Review D, 2019
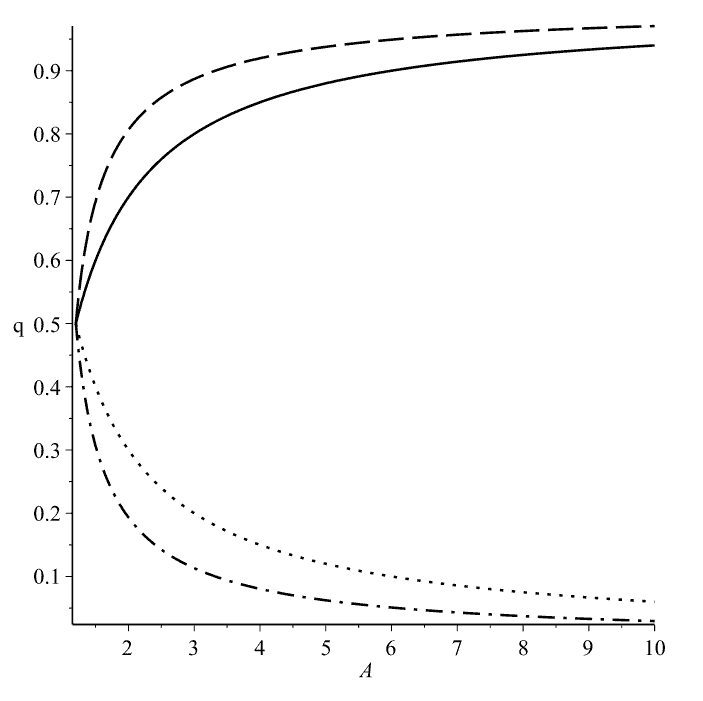
It turned out that due to the tunneling of the field through the wormhole in “our” space, it acquires a charge Q 1 = – qR / 2 A , where R is the radius of the hole. The “other” space it acquires charge Q 2 = – qR / 2 A . It turns out that the wormhole “takes” part of the charge and transfers it to the opposite end of the hole. The closer the charge is located to the border of the wormhole, the stronger this effect. If the charge also moves, then it can induce higher moments in the wormhole — for example, when the hole moves in a circular motion, it will acquire an apparent dipole moment.
De-Chang Dai & Dejan Stojkovic / Physical Review D, 2019
Then the physicists considered a slightly more realistic case – a wormhole connecting two black holes, that is, two spacetime with the Schwarzschild metric. Obviously, such a wormhole will be passable only if its radius is greater than the gravitational radius black hole. Against the background of such space-time, scientists placed a point source of a scalar field, examined the corrections arising against the background of a wormhole, and glued the fields at the border of the hole. The scalar field strength in “our” and “other” space, calculated with this formulation of the problem, resembled the electric field strength in a more naive example. However, this time the effect was expressed a little weaker. In addition, the effect completely disappeared if the radius of the wormhole coincided with the gravitational radius of the black hole.
In the framework of the same approach, scientists considered the “leakage” of the gravitational field of a point particle located next to a wormhole. As a result, physicists have found a correction for the acceleration, which will be experienced by an observer hanging over a wormhole in “our” space. ” Interestingly, in this case, the acceleration remained nonzero even if the radius of the wormhole and the gravitational radius of the black hole coincided.
De-Chang Dai & Dejan Stojkovic / Physical Review D, 2019
Finally, the researchers suggested that the black hole Sgr A *, located in the center of the Milky Way, is actually a wormhole with a radius approximately equal to the gravitational radius of the hole. In addition, scientists suggested that a star with an unknown mass and long semi-axis rotates around a wormhole in an “other” space in an elongated orbit. Since such a star should affect the motion of stars in “our” space, deviations from GR predictions may indicate the “mole” nature of Sgr A *.
Of course, with the current accuracy of observations, the motion of stars around the black hole Sgr A * fits into the framework of the General theory of relativity. For example, if we take the star S2 as the “test” object , the acceleration of which is currently measured with an accuracy of about 0.4 millimeters per second squared, the limitations are rather weak. Nevertheless, in the near future, astronomers can reduce the measurement error by about one to two orders of magnitude. With such accuracy, lighter and more distant stars from the “other” space will affect the S2 motion. Therefore, the authors hope that with the help of their predictions one day they will be able to verify whether Sgr A * is a wormhole.
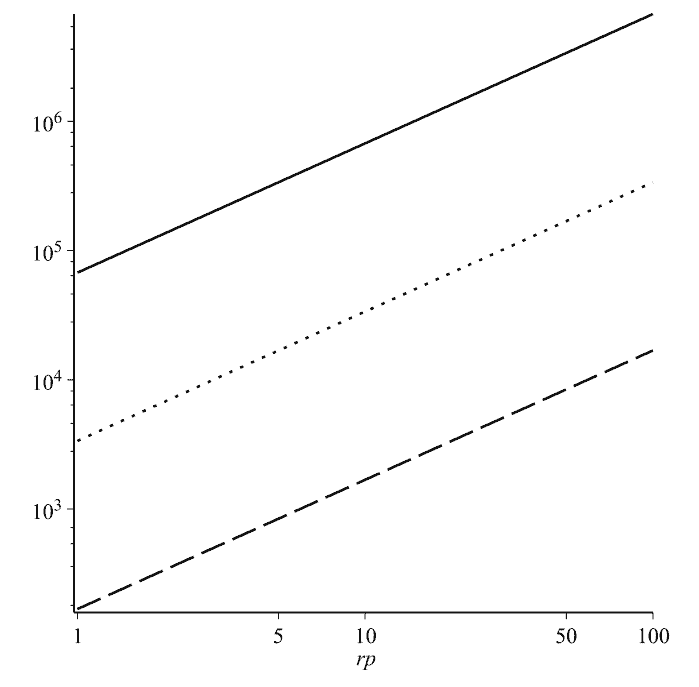
De-Chang Dai & Dejan Stojkovic / Physical Review D, 2019
Further details can be explored on Physical Review D.